管道修复人的圈子

引言

随着我国西部大开发“西气东输” “西油东送”等工程的发展和快速推进，输油输气管道的安全性深切关系着国计民生，已成为一项重要的研究课题；近年来，公路货运需求与日俱增，公路运输网逐年扩张,使得有越来越多的地上临时公路运输线与地下管道交叉，交通量大、载重量高、车速快等都成为危害管道安全可靠性的重要因素。

现阶段在进行管道设计时，重点仍是放在对管道截面的计算设计上,先将上部作用荷载简化为静载，采用Boussinesq解求解管顶附加应力，进而计算管道横截面的变形，据此进行管道设计。尽管从设计和计算的角度来看，此方法计算简单，但其只侧重考虑了管道环向应力，而忽略了管道纵向应力的计算，实际上管道纵向应力也是影响管道安全性的重要指标。

在管道纵向应力计算方面，主要基于Winkler弹性地基梁模型，国内外学者已经有诸多此方面的研究。20世纪70年代Parmelee等首次提出弹性地基梁模型；龙驭球的《弹性地基梁的计算》一书中详细介绍了弹性地基梁的特点及地基模型的分类，并细致推导了集中荷载作用下不同类型地基梁的计算公式；Rajani等[基于Winkler弹性地基梁理论，考虑温度影响和内压作用，建立了管道纵向受力模型；张土乔等对垂直荷载作用下的管道纵向受力模式进行探讨，建立了简化的受力模型并进行计算。目前对弹性地基梁理论的研究已经较为成熟，已成为较为公认的计算管道纵向应力的方法。

在动力响应研究方面，越来越多的专家学者开始关注动力效应问题。Datta采用薄壳模型研究了管线在地震作用下的力学响应；黄晓明研究了车辆在不同车速时所产生的路面交通载荷，分析车—路耦合作用；李洵对交通荷载作用模型进行简化，从而运用数值模拟软件进行埋地管道的力学性状研究；李新亮等进行了埋地管道的受力分析，并通过现场测试进行验证。时刚等通过室内模型试验，研究了地下管线渗漏与交通荷载综合作用下的路面塌陷的形成机理和影响因素。

目前国内外的研究大多仅停留在理论及数值模拟计算方面，鲜有学者进行现场试验进行验证，理论计算缺乏说服力；另一方面，运用Winkler弹性地基梁模型对管道纵向应力直接计算过程较为繁琐，工作量大且容易出错。因此，本文主要工作是进行理论计算的简化，并通过现场试验和数值模拟对理论计算进行检验和修正，提出简洁有效的方法。

1.理论计算

1.1 管顶附加应力计算

根据布辛内斯克(Boussinesq)解[7],在弹性半无限空间表面作用竖向矩形均布荷载时，可以求解角点下的附加应力，按式(1)计算。再根据荷载的分割和叠加，可以计算空间内任意一点的附加应力。

车辆荷载通过车轮作用于管道上方，将其简化为按左右轮分布的矩形均布荷载，计算模型如图1所示。图中，h为管道埋深；θ为应力扩散角；s为附加应力影响宽度，在宽度s以外可不考虑附加应力。

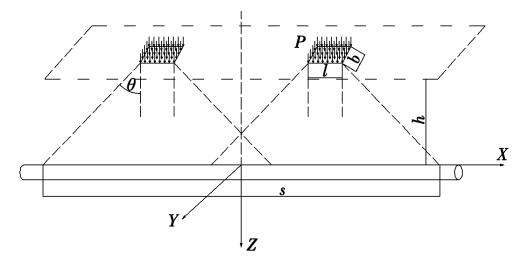
图1 附加应力计算模型

利用布辛内斯克解及应力叠加原理，可计算各位置的管顶附加应力。对计算结果进行整理，发现在对称矩形均布荷载的作用下，不同深度处附加应力分布形式有所区别。随着管道埋深的改变，管顶附加应力的分布形式也发生变化。

当管道埋深较浅时，荷载影响明显，车轮下方应力较大，管顶附加应力分布大致呈“马鞍型”,如图2中曲线h1所示；随着管道埋深增加，附加应力在管中的叠加更为明显，车辆中轴与车轮碾压位置应力值接近，如曲线h2所示； 埋深继续增加，管顶附加应力分布大致呈“驼峰型”,在车辆行驶中轴位置取得应力极值，如曲线h3所示。(h1< h2< h3)

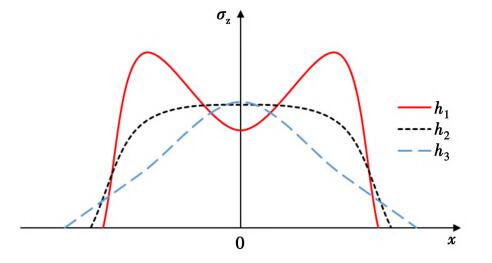
图2 管顶附加应力分布形式

1.2 Winkler弹性地基梁理论

Winkler弹性地基梁模型是考虑地基土体对梁体的支承作用，将地基土模拟为刚性支座上一系列独立的弹簧，通过梁的挠曲线微分方程求解外荷载作用下梁的内力。弹性地基梁模型如图3所示。

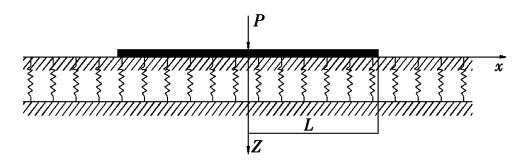
图3 弹性地基梁计算模型

在计算交通荷载作用下埋地管道纵向应力时，需要将交通荷载产生并传递到管顶上方呈曲线形式分布(图4实线所示)的附加应力积分，才能计算各个位置管道的内力，计算过程繁琐且容易出错，工作量较大。因此提出对上述3种附加应力分布形式分别按不同方式简化，如图4虚线所示。

如图4(a)所示，管道埋深较浅时，将附加应力简化为三角形与矩形分布荷载叠加；管道埋深增加，取管中和车轮处的较大值，将两车轮中间部分简化为矩形均布荷载，车轮外简化为三角形均布荷载；管道埋深继续增加，简化为2个三角形分布荷载。此时，只需求解三角形和矩形均布荷载作用下的弹性地基梁内力即可。

考虑Winkler弹性地基梁模型，梁的挠度曲线微分方程式为:

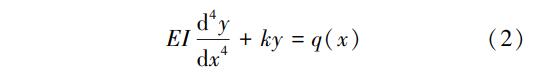
式中：EI为管道轴向抗弯刚度；k为地基系数；q(x)为梁上外荷载分布函数。

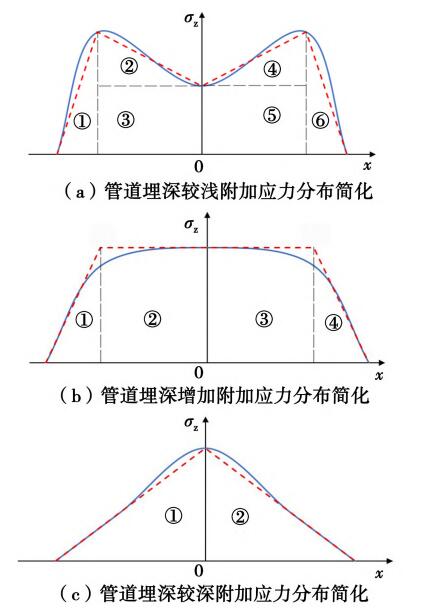
图4 附加应力简化示意图

引入特征系数α,满足：

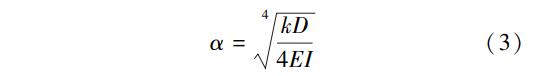
式中：D为荷载分布宽度。在计算中取为管道外径。

引入换算长度λ对弹性地基梁分类：

λ=αL         (4)

式中：L为荷载距管端距离，如图3所示。当1<λ<2.75时梁为短梁，λ>2.75时梁为无限长梁。

1.2.1 短梁求解

如图5所示，是三角形和均布荷载分别作用下弹性地基梁短梁计算模型。

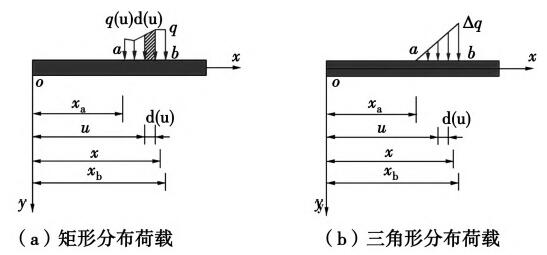
图5 分布荷载作用下短梁计算模型

图5(a)所示为梁上作用由矩形分布荷载时，梁内力计算模型，计算时将矩形分布荷载微分为长度为u的小段，按集中荷载计算后累积叠加。

计算可得，当xa≤x≤xb时：

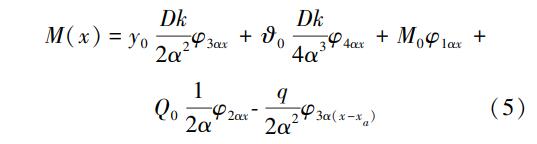
当x≥xb时：

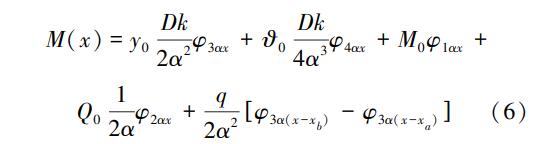
式中(下同):

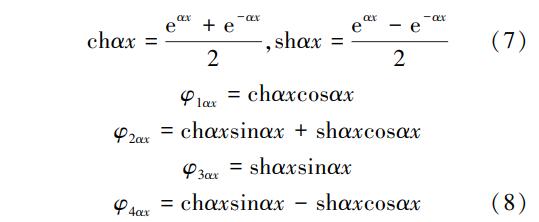
式中：y0、ϑ0、M0、Q0分别为x=0位置处的位移、转角、弯矩和剪力；xa、xb分别为矩形分布荷载开始作用和作用结束。

如图5(b)所示，当短梁上作用有三角形分布荷载时，与作用矩形均布荷载类似，都是将分布荷载微分成宽度为u的小段后，按集中荷载作用计算叠加。计算可得，当xa≤x≤xb时：

当x≥xb时：

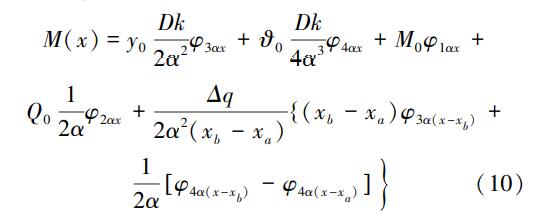
首先确定梁两端固定形式，确定梁端参数，之后可根据式(5)—(10)及弯矩、剪力、转角、位移的相关关系求解计算。

1.2.2 无限长梁求解

对于无限长梁在进行计算时，假定梁长趋向于无限长，梁端位移为零。如图3的弹性地基梁计算模型所示，当L趋向于无穷大，梁上作用有集中荷载时，可求解得出无限长梁各处的弯矩为：

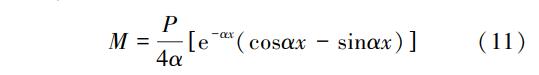
当无限长梁上作用有矩形或三角形均布荷载时，由于假定了梁长趋于无限长，而均布荷载分布宽度较小，因此计算时可将分布荷载积分，视作集中荷载作用来计算。

2.现场试验

选择典型场地开展模型试验，实地测量车辆行驶通过管道时，管道纵向应力的变化情况，与理论计算结果对比。

2.1 试验工况

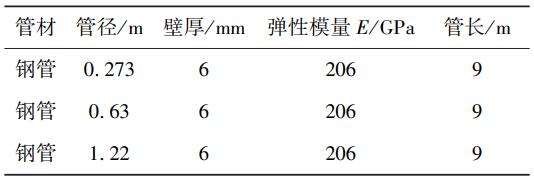
试验用管选用热轧薄壁圆形钢管，主要尺寸及力学指标见表1。

表1 试验用管技术指标

试验车辆选用如图6所示的双桥载重汽车，轮距为1.8 m, 现场装土，车辆满载时测得车辆重为42.10 t, 车辆后轴重27.50 t。根据《公路工程技术标准》规范规定，重型车辆荷载可简化为2个l×b=0.6 m×0.2 m矩形均布荷载，两荷载间距1.8 m, 现场车轴重对应的均布荷载大小为572.92 kPa。

图6 试验车辆

《输油管道工程设计规范(附条文说明)》规范规定，管顶上覆土层厚度不得小于0.8 m, 故现场按管道埋深0.8 m、1.2 m和2.4 m布置。0.273 m、0.63 m、1.22 m管径的管道所对应的开挖宽度分别为1m、2m和3m, 管道放置合适后用现场开挖土回填，控制含水率接近最优含水率，压实度控制为0.85。

2.2 应变片布置

本试验购置应变花测量管道应变。图7所示是应变花的布置位置图，在管道4个截面的管中、管侧和管底分别布设，截面分别为1-1车辆行驶中线；2-2车辆行驶车轮位置；3-3车轮作用位置外1 m; 4-4车轮作用位置外2 m。

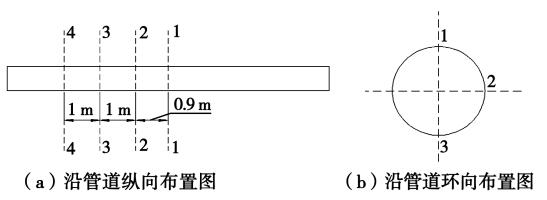
图7 应变片布置示意图

如图8所示，是应变花粘贴示意图，0°方向应变片所测试结果即为管道纵向应变。

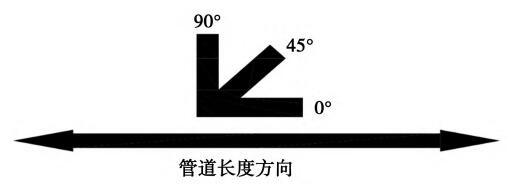
图8 应变片测试方向示意图

2.3 测试结果

如图9所示，是仪器采集并经数字滤波处理的管道应变时程曲线(埋深1.2 m、管径0.63 m)。

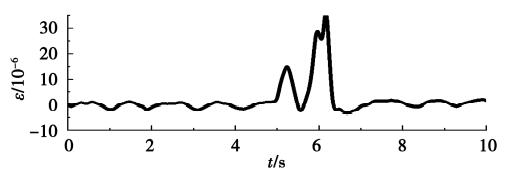
图9 管道应变时程曲线

试验时控制车辆以30 km/h的速度匀速行驶通过管道，动应变采集仪实时采集车辆行驶通过管道时的管道应变。

由图9可见，车辆行驶通过管道时，汽车前后轴依次碾压造成的管道变形清晰可见。提取管道应变峰值并乘以钢管的弹性模量，可以得出各个测点的纵向应力。

以管中位置为x轴零点，距离管中位置的距离为横坐标(向左为负，向右为正),以管道纵向应力值为纵坐标，绘制管道纵向应力沿管道分布规律图。现场应变采集仪测试通道有限，故应变片只在管中左侧布置，认为管道在车辆作用下应力关于管中截面对称分布，可轴对称得出右侧点的应力。

如图10所示，(a)(b)分别为实测管径0.63 m管道在不同埋深时管顶及管侧纵向应力分布。

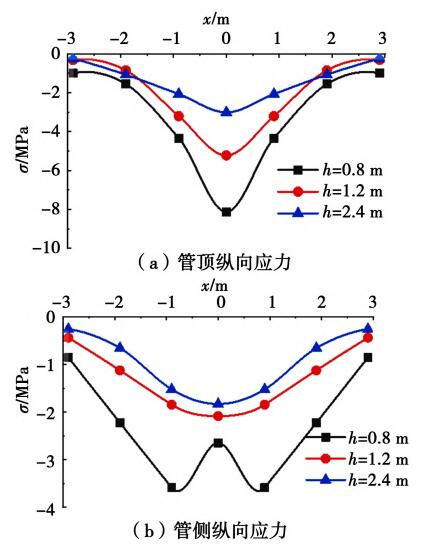
图10 实测管道纵向应力分布

由图10可见，管侧纵向应力明显小于管顶，且管顶纵向应力分布规律与梁在均布荷载作用下的受力状态较为接近。

3.数值模拟

由于现场试验条件有限，埋设的钢管长度仅为9 m, 为更接近工程实际，本节运用Midas GTS NX软件进行数值模拟计算。

3.1 计算工况

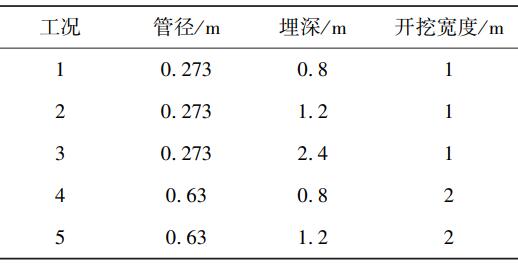
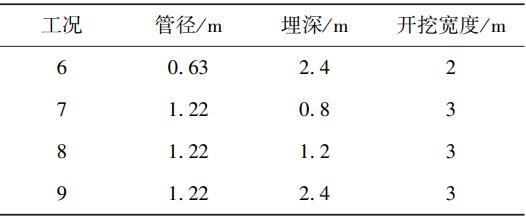
数值模拟工况与现场试验工况类似，计算工况如表2所示。

表2 数值模拟计算工况

3.2 模型建立

模型尺寸为10 m×10 m×30 m, 钢管长30 m, 模型如图11所示。回填土宽度按表2选取。

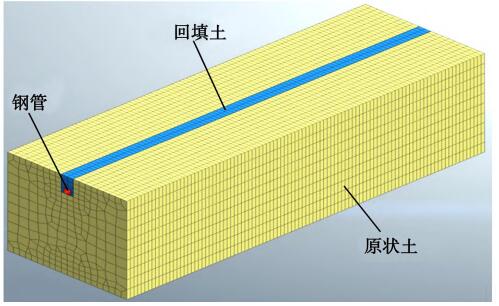
图11 计算模型

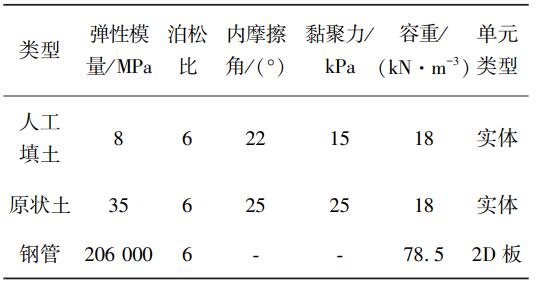
查阅相关资料,确定模型中材料参数如表3所示。

表3 模型参数

3.3 计算结果

如图12所示，是运用Midas软件计算工况5所得的管道变形及管顶纵向应力分布曲线。

由图可见，管顶纵向应力沿管中截面对称分布，在管中位置取得极值，管中变形最大，与现场管道的测试结果反映的规律一致，与梁在均布荷载作用下的变形及受力状态接近。

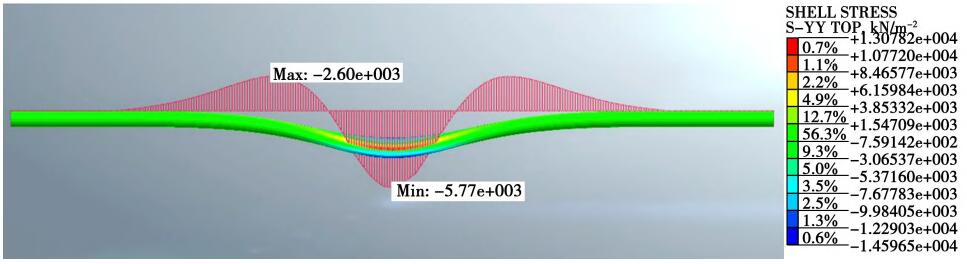
图12 数值模拟计算结果

4.结果分析

根据式(4),现场试验中管长为9 m, 经计算换算长度1<λ<2.75,属于短梁；数值模拟中管长为30 m, 计算所得的换算长度λ>2.75,为无限长梁。故将现场实测和数值模拟结果分别与按弹性地基梁短梁和无限长梁计算的结果进行对比。

4.1 结果对比

对比按弹性地基梁短梁计算所得与现场实测的管道纵向应力。如图13(a)所示，是管径为0.63 m、不同埋深的管道纵向应力计算与实测结果的对比。图13(b)是埋深为1.2 m、不同管径的管道纵向应力计算与实测结果的对比。(取应力扩散角为30°,地基系数为4×10⁷N/m³,绘图坐标意义同图10)

对比按弹性地基梁无限长梁计算与数值模拟计算所得的管道纵向应力。与短梁类似，图14(a)是管径为0.63 m、不同埋深的管道管顶纵向应力计算与数值模拟结果对比。图14(b)是埋深为1.2 m、不同管径的管道管顶纵向应力计算值与数值模拟结果对比。(取应力扩散角为30°,地基系数为4×10⁷N/m³,绘图坐标意义同图10)。

由图13中短梁理论计算结果与现场实测结果对比可见，理论计算与现场实测结果显示的管顶纵向应力分布规律一致，随管径与埋深变化规律一致；图14对比了无限长梁理论计算与数值模拟计算结果，同样管顶纵向应力分布规律一致，且随管径与埋深变化规律一致。证明了运用Winkler弹性地基梁模型计算管道的纵向应力是合理的。

图13 计算与实测管道纵向应力对比

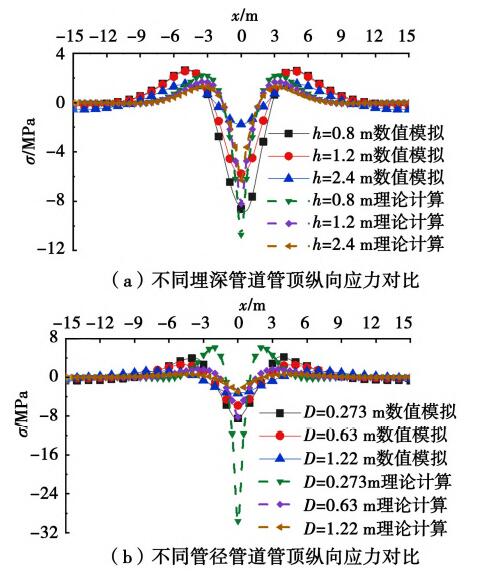
图14 计算与数值模拟管道纵向应力对比

理论计算、现场实测与数值模拟结果均表明：在交通荷载作用下，埋地管道管顶的纵向应力会在车辆作用中轴处取得极值。管顶应力峰值会随着管道埋深的增大而减小，随管道管径的增大而减小。

4.2 计算参数影响

在理论公式中，涉及到应力扩散角及地基系数这两个重要参数的取值，会对计算结果产生一定的影响。

4.2.1 应力扩散角

我国的《建筑地基基础设计规范(附条文说明)》(GB 50007—2011)及相关资料为地基压力扩散角的取值给出了一般建议值，按表4选取。

表4 应力扩散角取值

表4中：Es1为上层土压缩模量；Es2为下层土压缩模量；z/b<0.25时θ取0°;z/b>0.50时θ值不变；0.25<z/b<0.50时θ由插值法确定。

如图15所示，(a)、(b)分别为应力扩散角取不同值时，按弹性地基梁短梁和无限长梁计算所得管顶纵向应力计算值与实测及数值模拟的对比。(以管径0.63 m、埋深1.2 m工况为例，地基系数取4×10⁷ N/m³,绘图坐标意义同图10)

在图15中，通过对比发现，应力扩散角分别为23°、25°和30°时，按弹性地基梁不同模型计算所得的管顶纵向应力结果均很接近，证明应力扩散角的取值对管顶截面纵向应力的影响效果较小，扩散角较大时的计算结果略大。

4.2.2 地基系数

地基系数取值的确定比较复杂，与基底压力大小及分布、土的压缩性、土层厚度、外荷载等息息相关，受多种因素的影响。缺乏相关试验数据时可以查阅相关资料近似取值，如顾晓鲁等主编的《地基与基础》一书中就根据土体分类给出了地基系数参考值。天然地基黄土及黄土类粉质黏土k值可取4.0×10⁷～5.0×10⁷ N/m³。

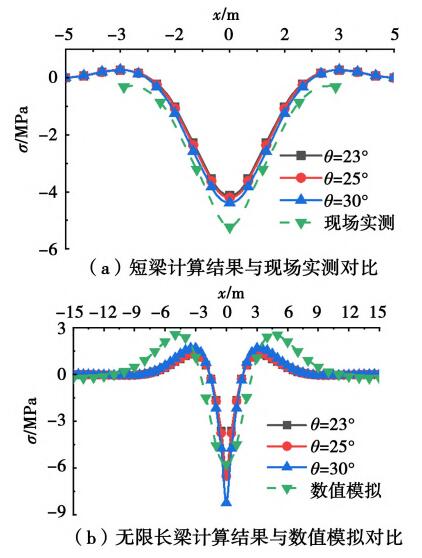
图15 θ取不同值时管顶纵向应力计算

如图16所示，(a)(b)分别为地基系数取不同值时，按弹性地基梁短梁和无限长梁计算所得管顶纵向应力计算值与实测及数值模拟的对比。(以管径0.63 m、埋深1.2 m工况为例，应力扩散角取30°,绘图坐标意义同图10)

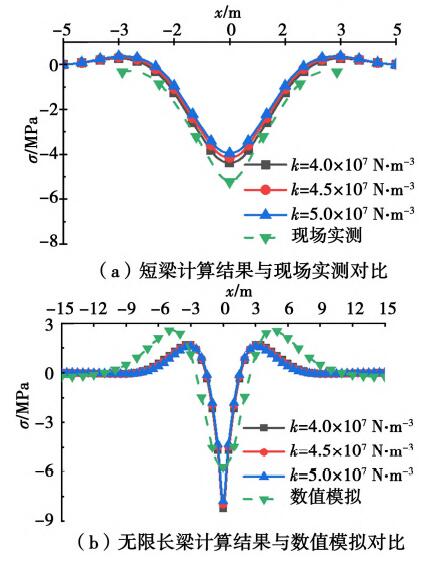
图16 k取不同值时管顶纵向应力计算

如图16所示，地基系数分别取4.0×10⁷ N/m³、4.5×10⁷ N/m³和5.0×10⁷ N/m³时，短梁与无限长梁计算所得的管顶纵向应力峰值均变化不大，总体上看，地基系数较小时计算所得的纵向应力较大。

4.3 动力效应

由上文中理论计算与现场实测结果对比图可见，管道纵向应力的理论计算结果总是小于现场实测。这是由于在理论计算时，是将交通荷载简化为静载进行的计算，而现场由于路面不平顺等诸多原因，车辆行驶会产生动力效应,仅仅使用理论计算结果进行管道设计是不安全的。因此本文通过动力影响系数对理论计算结果进行修正，即：

σ′=Kσ         (12)

式中：σ′为修正后埋地管道纵向应力；σ为按Winkler弹性地基梁模型计算所得理论解；K表示交通荷载作用下的动力影响系数。

当K取不同值时，通过对比修正后的埋地管道纵向应力与现场实测值，来确定动力影响系数取值。如图17所示，是管径0.63 m、不同埋深位置的管道，当K取不同值修正后的管道纵向应力与现场实测结果的对比。

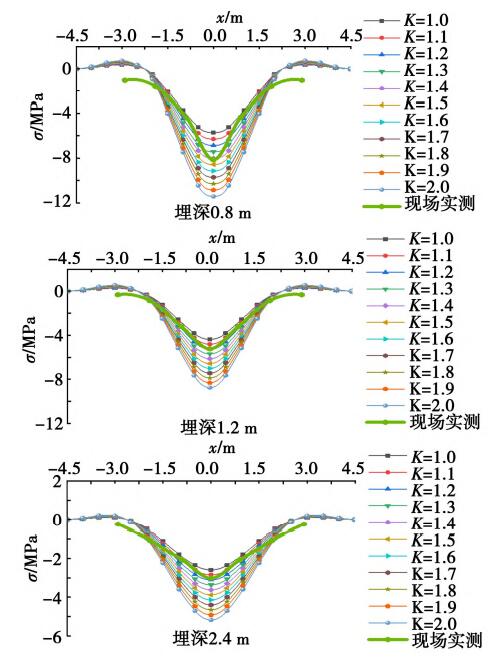
图17 理论计算修正后管顶纵向应力与现场实测对比

由图17可见，当管道埋深为0.8 m时，动力影响系数K约为1.5;当管道埋深为1.2 m时，K约为1.2;当管道埋深为2.4 m时，K约为1.1。因此为保守起见，在进行交通荷载作用下埋地管道纵向应力计算时，动力影响系数可取为1.5。

5 结论

(1)通过对比分析现场实验数据、数值模拟与理论计算结果，验证了运用弹性地基梁模型进行管道纵向受力分析的可行性，验证了简化计算方法的简洁高效。

(2)得出交通荷载作用下埋地管道纵向应力分布规律。管道纵向应力在车辆作用中心处取得峰值，且应力峰值会随管道埋深和管径的增大而减小。

(3)理论计算中，附加应力扩散角与地基系数的取值对管顶纵向应力峰值影响不大。扩散角较大时应力计算结果略大，地基系数较大时应力计算结果略小。

(4)由于存在路面不平顺等情形，车辆作用在管道上时存在动力影响，故引入动力影响系数K对计算结果加以修正，本文对比理论计算修正结果与现场实测数据，得出在进行交通荷载作用下埋地管道纵向应力计算时，动力影响系数宜取为1.5。

摘自《地下空间与工程学报 》